一直有一个疑问，iPhone的闹钟响了后，再睡一会，为什么是会等待9分钟后再次响起？为什么不弄个10分整呢，或者6分钟也行啊（一小时的1/10），特别是强迫症患者（悲痛）。
早期的钟表是齿轮式的，因此很难准确地设置10分钟的贪睡时间。 因此，他们的目标是少于10分钟，也就是9分钟。 直到50年代，这都是相当标准的事情。
Telechron 是最早生产待贪睡功能的闹钟厂商之一。
当时的那个带Snooze的闹钟
虽说是电子表，但据称控制snooze的齿轮是9齿的，所以实现9分钟比较容易。
对先辈的致敬。
当闹钟响起时，第一分钟也已经开始了，如果闹钟最多响1分钟的话，增加9分钟其实就刚好10分钟后起床。
难怪有人说，9分钟的瞌睡已经是一个业界标准了，但成因是众说纷纭的。Apple将这个半个多世纪前，小睡一会应该是多久的公认标准保留到了现在。
你觉得如何呢？上面可有一个理由说服你？
前天在Twitter上看到个数学题，据称是小学的，想了很久 🙂
题目如下：
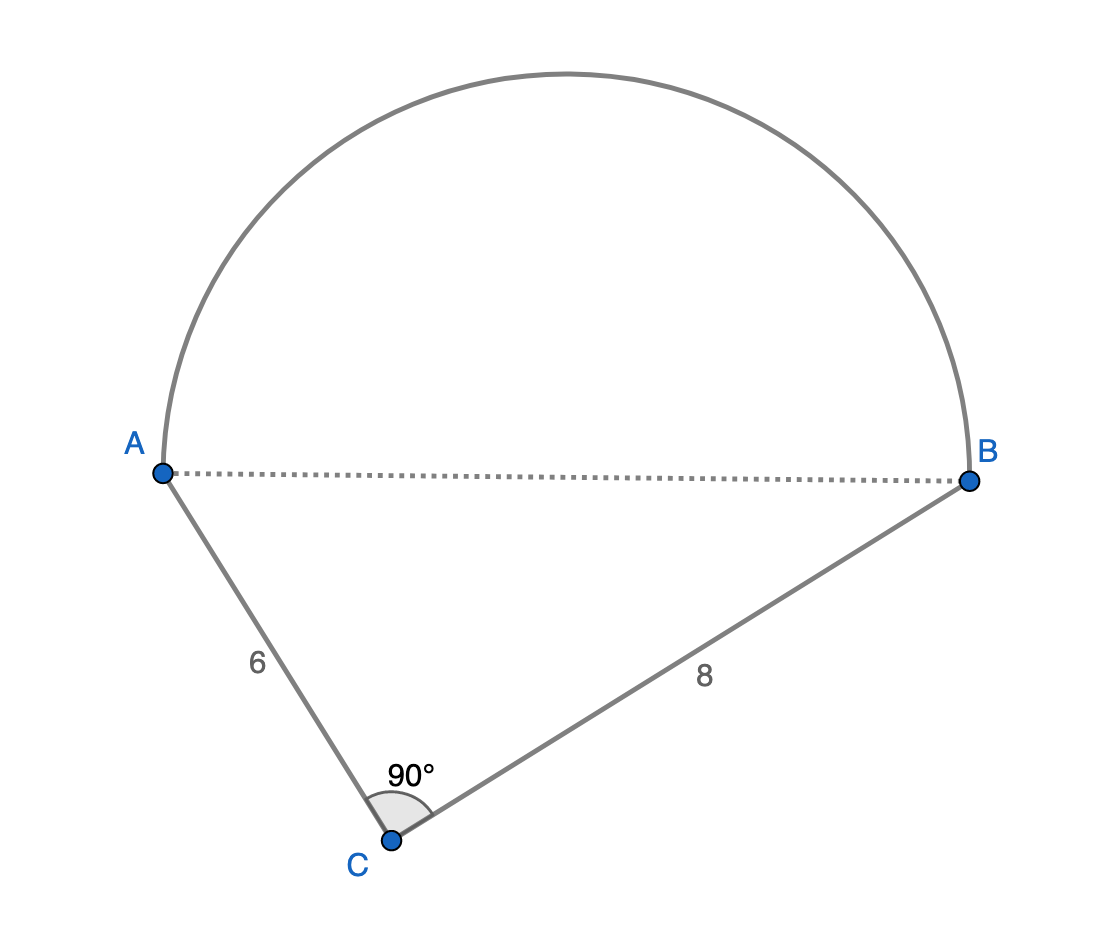
一个直径为10的半圆，和一个三边长分别是6，8，10的三角形，拼成如图的图形。请作一条直线，将此图形分成面积相等的两部分。
这个问题当然有无数多个解，但如何找到一个简单的答案呢？
方法1：
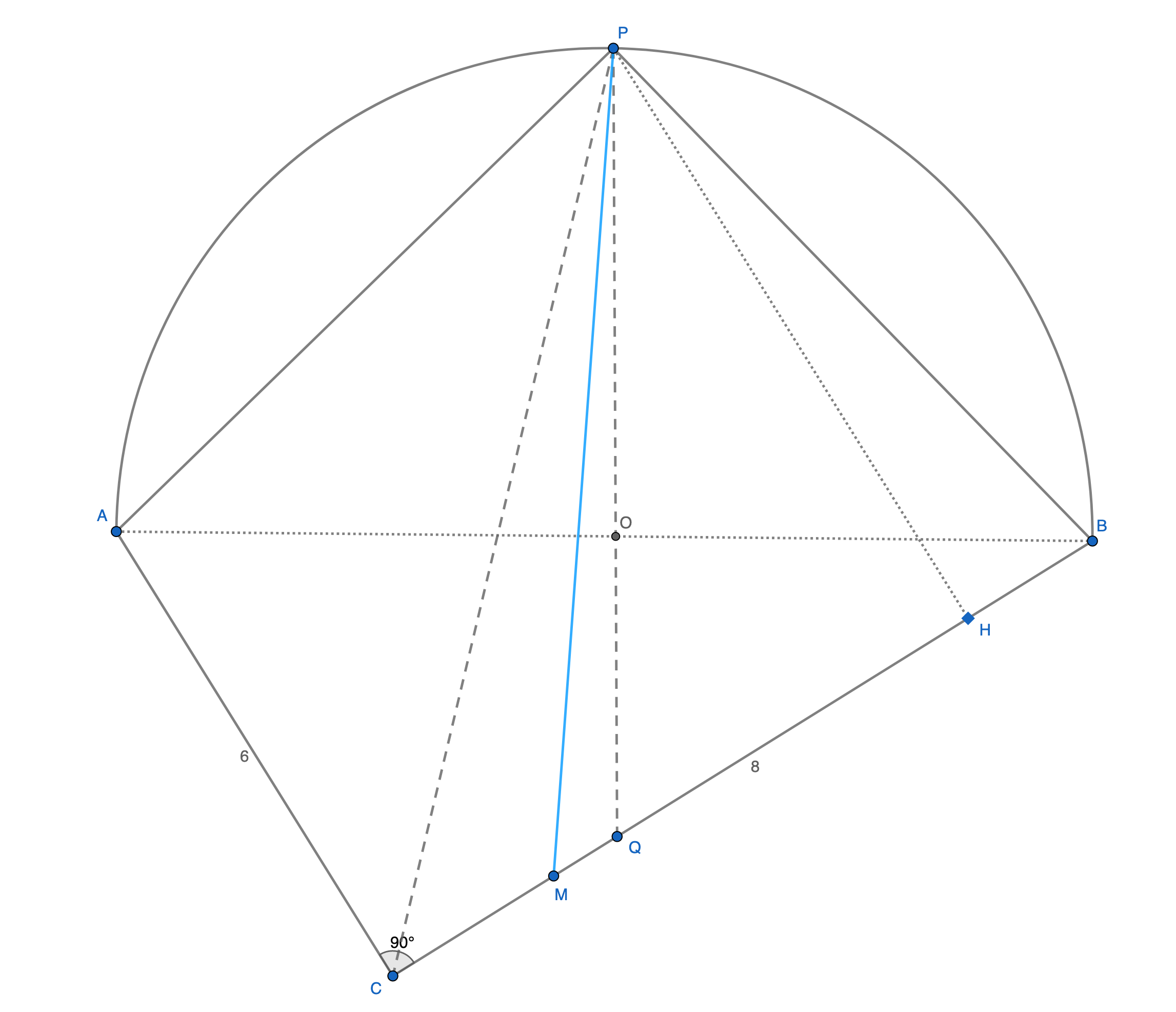
在圆心O处，作AB的垂线，交圆于P，交BC于Q。
连接PQ，那PQ左边的图形面积显然大于PQ右边的图形面积。
连接PC，那PC左边的图形面积显然小于PC右边的图形面积。
所以如果这条分割点是经过P点的那一条，那么它和图形的另一个交点在C和Q之间，设其为M。直线PM将图形分成面积相等的两部分。
由于弧PA=PB，所以PB和PB两个饼状部分面积相同。所以直线PM将四边形PACB分成面积相等的两部分。
四边形PACB的面积是三角形PAB和三角形ABC的和，即S=1/2*5*5 + 1/2*6*8 = 49
设PH垂直于BM。
我们知道△BOQ和△BCA相似，所以OQ/OB=AC/BC，即OQ=AC/BC*OB = 15/4
BQ = OQ*5/3 = 25/4
S△BPQ = 1/2 * PQ * OB = 1/2 * BQ * PH
所以 PH = PQ * OB / BQ = (5+15/4) * 5 / (25/4) = 7
所以 S△BPM= 1/2 * BM * PH = 49/2
BM = 7
方法2
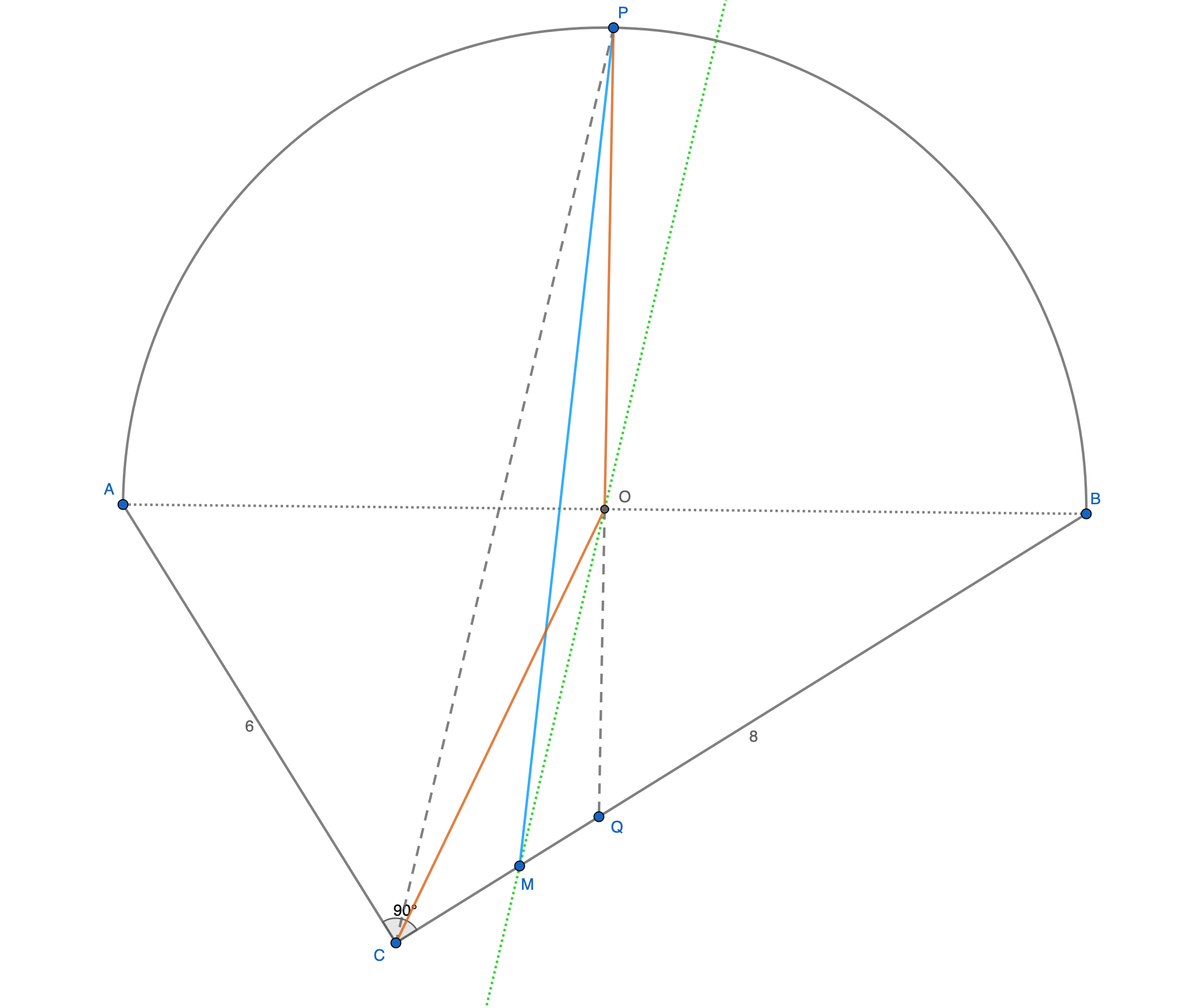
我们连接PO，那么PO将半圆分成面积相等的两部分。我们连接OC，那么OC将三角形ABC分成面积相等的两部分。
但可惜PO、PC不共线。
我们可以看到，PO，PC右边部分面积（图形的一半面积）S1=S⌔POB+S△OBQ+S△OCQ。
我们连接PC，然后过O作PC的平行线，交BC于M。
PM右边的部分面积 S2 = S⌔POB + S△OBQ + S△PMQ。
而，
S△PMQ/S△PCQ = MQ/CQ，
S△OCQ/S△PCQ = OQ/PQ。
由于OM与PC平行，有MQ/CQ=OQ/PQ，所以S△OCQ = S△PMQ。
所以S2 – S1 = S△PMQ – S△OCQ = 0，
所以PM也将图形分成了面积相等的两部分。
这个方法就不用算算算了。
金庸去世了，留下了很多作品。突然想起今年印象最深的几句话：
一个人停止创造内容了，对世界就没有价值了。
人死之后，唯一留下的，就是艺术。
我应该是那种可以快速感兴趣的人。之前有人说我是好奇宝宝，是有三分钟热度，却浅尝辄止的那种孩子。就像很多年前去学素描、去攀岩、去骑车等。但开始之后，也许慢慢就失去兴趣了，或者没有放很多精力在上面。就像我经常说自己很喜欢钓鱼，可真有休闲时，有多少时候真的会出门呢。恐怕有点叶公好龙吧，懒癌果然是无药可救的。
最近几年坚持比较久的活动，应该就数2015年时去考了司法考试，也是情不知所起吧，没想到竟然真的能考出来（虽然没啥用😂）。
今年9月底去开始在上的法语语音课。希望自己可以坚持下去，而不是不停的挖坑。今年挖的坑：健身，素描，法语，书法。
不容易坚持的人永远都不会幸福吧，在这给自己立个小目标，小flag。
